TEMA I: TEORIA DE ERRORES EN LAS MEDICIONES
La teoría de errores constituye una rama del conocimiento científico que, a los efectos de la enseñanza, queda en un terreno intermedio entre el de las teorías científicas y el de la práctica experimental.
En cursos teóricos (Teoría de los Números Aproximados, Cálculo Diferencial, Estadística) se analizan, en forma disgregada, elementos de la Teoría de Errores (confiabilidad de las cifras, cálculo con cantidades pequeñas, desviaciones probables, etc.), con un enfoque más cercano a los muestreos poblacionales de parámetros sociales y económicos que al de la instrumentación científica. Por otra parte, en los laboratorios docentes la preocupación fundamental de los profesores radica en las técnicas Instrumentales y en la verificación experimental de leyes, analizadas en los cursos teóricos de la ciencia correspondiente. En cada experimento se sugiere al estudiante valorar los errores que más influyen en él, explicitando estos en cada caso: a veces, errores casuales, a veces, sistemáticos rectificables; otras veces, errores de apreciación de los instrumentos; otras, los de método. Y el estudiante va adquiriendo una visión fragmentada de todos los tipos de errores, pero sin una clara noción de cómo se vinculan, y cuándo tener en cuenta sólo a unos y no a los otros.
Los métodos para procesar todos estos tipos de errores se van analizando también disgregadamente, de acuerdo con cada experimento específico estudiado, y de acuerdo con el enfoque del profesor de cada laboratorio.
En fin de cuentas, el modo de evaluar los errores y el de procesarlos es, a veces, tan variado como lo sean los profesores por los que ha pasado un estudiante. Y se espera que éste, ya sea científico o ingeniero, adquiera la formación correcta en el tratamiento de los errores de medición.
Un paso fundamental en la enseñanza de un tema, o asignatura, con enfoque sistemático, es dejar establecida al inicio, en forma de recuadro, la estructura completa del contenido a tratar, que muestre los vínculos y engranajes de unas partes con otras, y explicar, sin profundidades, en qué consiste cada parte. Después, durante el curso, se estudia cada parte consignada en el recuadro inicial, que se retoma durante el curso tantas veces como se requiera.
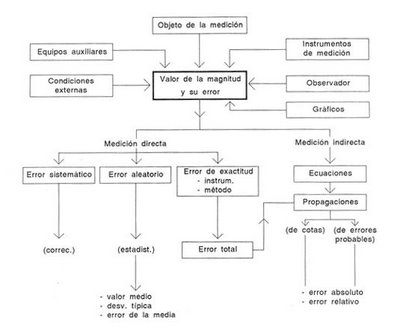
Incertidumbre de las Medidas
La limitación de los elementos físicos disponibles para realizar un sistema de medida hacen que las señales de salida discrepen de las que se obtendrían con un sistema ideal. Estas discrepancias se denominan errores y, dado que algunas de ellas son inevitables, el objetivo es reducirlas de modo que a partir de la salida se pueda determinar el valor de la entrada con una incertidumbre aceptable. El número de cifras con que se exprese un resultado debe concordar con la incertidumbre que tenga asociada.
Los errores de un sistema se determinan a partir de su calibración, que consiste en aplicarle entradas conocidas y comparar su salida con la obtenida con un sistema de medida de referencia, más exacto.
Las medidas nunca permiten obtener el “verdadero valor” de la magnitud que se mide. Esto es debido a multitud de razones. Las más evidentes son las imperfecciones, inevitables en un cierto grado, de los aparatos y de nuestros sentidos. El “verdadero valor” de una magnitud no es accesible en la realidad y por ello resulta más propio hablar de estimaciones, medidas o aproximaciones del valor de una magnitud. Independientemente de estas consideraciones, en el ámbito de la Instrumentación se sabe que no tiene sentido hablar del valor de una magnitud, sino sólo de la probabilidad de obtener uno u otro valor en una determinada medida de esta magnitud. Esto no es el resultado de las imperfecciones de los aparatos, sino de la propia esencia de la naturaleza. Este carácter probabilístico de las magnitudes se hace patente a nivel microscópico.
La consecuencia de las consideraciones anteriores, es que toda medida es incierta o está dotada de un cierto grado de incertidumbre. Es esencial estimar ésta incertidumbre, primero porque el conocimiento de la incertidumbre aumenta la información que proporciona la medida, y segundo, porque este conocimiento permite manejar las medidas con la prudencia que dicta el conocimiento de la confianza que nos merecen.
Cuando se exprese el resultado de una medida es pues necesario especificar tres elementos: número, unidad e incertidumbre. La ausencia de alguna de ellas elimina o limita la información que proporciona.
Según su naturaleza los errores pueden ser sistemáticos o aleatorios.
Error Sistemático
Un error sistemático tiene siempre la misma amplitud cuando las condiciones del sistema son las mismas, o bien varía de acuerdo con una ley conocida cuando una de dichas condiciones cambia de una forma predeterminada.
Pueden surgir de emplear un método inadecuado, un instrumento defectuoso o bien por usarlo en condiciones para las que no estaba previsto su uso. Por ejemplo, emplear una regla metálica a una temperatura muy alta, puede introducir un error sistemático si la dilatación del material hace que su longitud sea mayor que la nominal. En este caso, todas las medidas pecarán (sistemáticamente) por defecto. El error podría evitarse eligiendo un material de coeficiente de dilatación bajo o controlando la temperatura a la que se mide.
Un error sistemático por ejemplo, son las resistencias reales del modelo del sistema de medida y que se suman o interfieren en el proceso de medida.
Medir temperaturas con un termómetro graduado en grados Farenhait, suponiendo por equivocación que está graduado en grados Celsius, introduce también un error sistemático en la medida. El error se evita en este caso recabando información sobre la escala del termómetro.
Los errores sistemáticos no son objeto de la teoría de errores. Realmente son equivocaciones que pueden y deben evitarse, empleando métodos e instrumentos de medida correctos y adecuados a los fines que se deseen obtener.
Error Aleatorio
Un error aleatorio tiene una magnitud que cambia de unas a otras ocasiones a pesar de que las condiciones del sistema sean las mismas.
Los errores aleatorios se manifiestan cuando se mide repetidamente la misma magnitud con el mismo instrumento y el mismo método, y presentan las siguientes propiedades:
Los errores aleatorios positivos y negativos de igual valor absoluto tienen la misma probabilidad del producirse.
Los errores son tanto menos probables cuando mayor sea su valor.
Al aumentar el número de medidas, la media aritmética de los errores aleatorios de una muestra tiende a cero.
Para un método de medida determinado, los errores aleatorios no exceden de cierto valor. Las medidas que lo superan deben repetirse y, en su caso, estudiarse por separado.
La calibración permite corregir los errores sistemáticos y estimar la magnitud de los errores aleatorios (pero no corregirlos).
Errores Estáticos y Errores Dinámicos
Según que se manifiesten cuando las señales de entrada son lentas o rápidas, los errores se denominan estáticos o dinámicos.
Un error estático afecta a las señales lentas, por ejemplo de frecuencia inferior a 0,01 Hz. Un error dinámico afecta a las señales rápidas, y es una consecuencia de la presencia de elementos que almacenan energía. Dado que en la respuesta dinámica se consideran dos fases, la respuesta transitoria y la respuesta estacionaria, se habla de error dinámico transitorio y error dinámico estacionario.
El error dinámico de un sistema depende de su orden y de la forma de la señal de entrada. Las señales consideradas habitualmente son el escalón, la rampa y las senoidales. Los sistemas de orden cero no tienen error dinámico. Los sistemas de primer y de segundo orden tienen un error dinámico para las entradas en rampa y senoidales, incluso en régimen estacionario, y tienen un error dinámico para las entradas en escalón sólo durante la fase transitoria. En los sistemas de segundo orden la fase transitoria dura tanto más cuanto menor sea el amortiguamiento. El error dinámico para entradas senoidales incluye un retardo y un error de amplitud, pero normalmente al hablar de error dinámico se suele sobrentender el error de amplitud.
Forma de expresar los errores
La magnitud de un error se puede expresar como error absoluto, como error relativo o como error referido a fondo escala. El error absoluto es la diferencia entre el resultado y el verdadero valor (o valor ideal). El error relativo es el cociente entre el error absoluto y el verdadero valor. El error absoluto se expresa a veces como porcentaje de una magnitud de referencia, por ejemplo el valor de fondo de escala. La elección de una u otra forma de expresión depende del tipo de error.
Error Absoluto
Por motivos obvios, y por su propia naturaleza, no es posible determinar exactamente un error. En el mejor de los casos, puede llegarse a una estimación de ese error. Cuando el resultado de una medida se expresa por:
lo que se quiere decir es que la magnitud medida se encuentran en el intervalo con una determinada probabilidad. Con una medida logramos acotar el intervalo de valores en los que se encuentra la magnitud que pretendemos medir, pero siempre con una determinada probabilidad. Es evidente que el error expresado por es una magnitud de la misma clase que la medida y se expresa por tanto con la misma unidad. También es claro que en las medidas de calidad normal el error debe ser mucho menor que el valor nominal, x. Por definición es siempre positivo.
Error Relativo
El error definido arriba se llama error absoluto. Tiene también interés el error relativo, que se define como el cociente del error absoluto, dividido por x.

En medidas de una cierta calidad el error relativo debe ser mucho menor que la unidad. Frecuentemente se expresa multiplicado por 100, con lo que aparece en tanto por ciento del valor medido:

Cifras significativas
Se considera que las cifras significativas de un número son aquellas que tienen significado real o aportan alguna información. Las cifras no significativas aparecen como resultado de los cálculos y no tienen significado alguno. Las cifras significativas de un número vienen determinadas por su error. Son cifras significativas aquellas que ocupan una posición igual o superior al orden o posición del error.
Por ejemplo, consideremos una medida de longitud que arroja un valor de 5432,4764 m con un error de 0,8 m. El error es por tanto del orden de décimas de metro. Es evidente que todas las cifras del número que ocupan una posición menor que las décimas no aportan ninguna información. En efecto, ¿qué sentido tiene dar el número con precisión de diezmilésimas si afirmamos que el error es de casi 1 metro?. Las cifras significativas en el número serán por tanto las que ocupan la posición de las décimas, unidades, decenas, etc, pero no las centésimas, milésimas y diezmilésimas. Cuando se expresa un número debe evitarse siempre la utilización de cifras no significativas, puesto que puede suponer una fuente de confusión. Los números deben redondearse de forma que contengan sólo cifras significativas. Se llama redondeo al proceso de eliminación de cifras no significativas de un número.
Una última forma de expresar el error de un número consiste en afirmar que todas sus cifras son significativas. Esto significa que el error es del orden de media unidad de la última cifra que se muestra. Por ejemplo, si el resultado de una medida de longitud es de 5432,8 m, y afirmamos que todas las cifras son significativas, quiere decirse que el error es del orden de 0,5 m, puesto que la última cifra mostrada es del orden de las décimas de metro.
¿Cómo pueden determinarse las cifras significativas a partir del número que expresa el error?. Hay que tener siempre presente que todo error es una estimación y está por tanto sujeto a su vez a una incertidumbre, generalmente grande. Por esto no tiene sentido especificarlo con excesiva precisión. Salvo casos excepcionales, se expresará con una sola cifra significativa. Sobre cómo redondear números, consultar la sección.
Redondeo de Números
Hemos visto que todos los números resultantes de una medida tienen una cierta incertidumbre. Es necesario eliminar de estos números aquellas cifras que carecen de significado porque el error es mayor que lo que estas cifras significan.
Este error es sin embargo excesivamente grande, además de que el criterio utilizado es discutible. Parece más apropiado tomar como error la desviación media, es decir, el valor medio de la diferencia de los datos respecto al valor central. Sin embargo, como los datos difieren tanto por defecto como por exceso del valor medio, tal desviación se aproximaría a cero. Para evitarlo suele tomarse, no el valor medio de las desviaciones, sino el valor medio de las desviaciones al cuadrado. De esta forma todos los sumandos son positivos. Para que la unidad de este número sea homogénea con la de los datos, se extrae la raíz cuadrada. El valor resultante se llama desviación típica o desviación estándar del conjunto de datos.

Cuando el número de datos es pequeño, suele preferirse el cálculo de la desviación estándar por la ecuación:

La primera suele llamarse desviación estándar de población, y la segunda desviación estándar muestral. Uno de los motivos de preferir la segunda, es que cuando medimos una sola vez, el resultado de la ecuación 6 es , es decir un número indefinido. Efectivamente, midiendo una magnitud una sola vez, no tenemos información alguna sobre su error, y por lo tanto éste debe permanecer indefinido. Sin embargo la expresión 5 conduciría a un error nulo.
Las dos expresiones se emplean, aunque en la práctica, y si el número de medidas es grande, la diferencia entre emplear una u otra es muy pequeña. La más empleada es la segunda, ecuación 6 y es la que usaremos nosotros.
Significado de la Desviación Estándar. La Distribución Normal
Los valores de la desviación estándar que hemos calculado en la sección anterior, son realmente estimadores de este parámetro. El conjunto de las medidas de una magnitud, siempre que exista un error accidental, pueden caracterizarse por medio de una distribución estadística. Cuando el error es debido a un gran número de pequeñas causas independientes, la distribución se aproxima a la llamada distribución normal.
La forma de representar en estadística una distribución es representando en abscisas el conjunto de valores que pueden obtenerse en una medida y en ordenadas la probabilidad de obtenerlos. En el caso de que la magnitud medida varíe de forma continua, en ordenadas se representa la probabilidad por unidad de intervalo de la magnitud medida.
La función de densidad de la distribución normal tiene el aspecto reflejado en la figura 4. Recibe también el nombre de campana de Gauss debido a su forma. Está caracterizada por dos parámetros: media y desviación estándar. La media es el valor que con mayor probabilidad aparecerá en una medida. La desviación estándar refleja lo abierta o cerrada que es la campana de Gauss correspondiente. Una distribución muy cerrada se corresponde con una serie de medidas muy poco dispersas, y por tanto con poco error. Por el contrario si la distribución es abierta, la desviación estándar es grande.
Una de las propiedades de la distribución normal es que la probabilidad que encierra en el intervalo es del 68.3 % aproximadamente. Es decir, es de esperar que el 68.3 % de las medidas de una magnitud estén comprendidas en ese intervalo. Dicho de otra forma, si medimos una magnitud un número grande de veces, el 68.3 % de los valores obtenidos estarán comprendidos en el entorno de una desviación estándar en torno a la media. La probabilidad se amplía al 95.4 % y al 99.7 % si consideramos los intervalos y respectivamente.
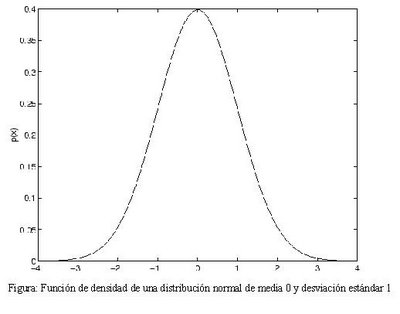
Figura 4: Función de densidad de una distribución normal
El error expresado por la desviación estándar tiene por tanto un significado probabilístico: hay una probabilidad del 68% de que una medida esté en el entorno de una desviación estándar alrededor de la media.
La distribución normal aparece con frecuencia en las medidas de magnitudes, pero no siempre. La distribución de una serie de medidas se aproxima a una normal siempre y cuando la fuente de error sea la superposición de muchas pequeñas causas independientes. Si hay una o varias causas de error predominantes o si las causas de error no son independientes, se dice que las medidas presentan un sesgo, y la distribución puede muy bien ser otra. Es muy frecuente encontrar distribuciones de medidas no simétricas, con dos o más máximos, etc.
Conviene insistir finalmente en que no es posible determinar la media y la desviación estándar de una distribución, sino solamente estimarlas.
Medidas sin dispersión. Error de lectura o instrumental
En ocasiones la repetición de la medida de una magnitud conduce siempre al mismo valor. Como ejemplo, consideremos la medida de la longitud de un objeto con una regla graduada en milímetros. Si la medida se realiza con cierta atención, todas las medidas del objeto proporcionan el mismo valor. Es evidente que en este caso la teoría anterior no resulta aplicable, porque al ser nula la dispersión, la desviación estándar resulta igual a cero. En estos casos, la fuente de error no está en la superposición de muchas causas aleatorias, sino en la sensibilidad del aparato de medida.
En efecto, el hecho de que todas las medidas sean iguales no indica en general que no haya error accidental, sino que éste es demasiado pequeño para quedar reflejado en el aparato. En el ejemplo anterior, si el error accidental de las medidas es del orden de 0,001 mm es evidente que la regla no podrá apreciarlo, resultando todas las medidas iguales. En estos casos es necesario estimar el error debido a la sensibilidad finita del aparato de medida.
Se llama sensibilidad de un aparato a la mínima variación de la magnitud medida que es capaz de detectar. En los instrumentos analógicos coincide frecuentemente con la mínima división de la escala. En el ejemplo anterior la sensibilidad de la regla es de 1 mm.
Suele llamarse apreciación al máximo error que puede cometerse debido a la sensibilidad del aparato. Generalmente se considera como la mitad de la sensibilidad. Esto puede comprenderse con un ejemplo. Supongamos un voltímetro de 0,1 V de sensibilidad, cuya aguja indica una tensión comprendida entre 2,1 V y 2,2 V, es decir, la aguja señala un punto intermedio entre las dos marcas o divisiones de la escala. Si el aparato está bien diseñado, una persona con apreciación visual media debe ser capaz de decidir si la aguja está más cerca de 2,1 V o de 2,2 V. Cometeremos el máximo error cuando la aguja se encuentre justamente en el centro de las dos divisiones. En tal caso el error de dar como lectura 2,1 V o 2,2 V es de 0,05 V, es decir la mitad de la sensibilidad.
Hemos visto que cuando el error instrumental es mucho mayor que el accidental, éste queda enmascarado por aquel. El efecto inverso es también posible. Por tanto, en los casos en que el error accidental de una medida sea mucho mayor que el instrumental, sólo consideraremos el error accidental.
Propagación de Errores
Las operaciones matemáticas con números inciertos dan lugar a resultados también inciertos, y es importante poder estimar el error de los resultados a partir de los errores de los números con los que se opera.
Consideremos un ejemplo sencillo para ilustrar este tema. Supongamos que se mide el lado (x) de una parcela de terreno cuadrada, y a partir de esta medida quiere obtenerse su superficie (y). La medida del lado llevará aparejada un error, que puede ser de origen accidental, instrumental o combinación de ambos. Admitamos que el lado mide 8 m y que el error es de 1 m. El valor de la superficie es por tanto de 64 m2, y estamos interesados en estimar su error.
El error en la medida del lado puede interpretarse como el radio de un entorno alrededor del valor nominal, en cuyo interior estará el valor del lado con una determinada probabilidad. Si proyectamos este entorno sobre la curva obtendremos otro entorno en el eje de ordenadas que representa el error de la superficie. Inspeccionando la figura llegamos a la conclusión de que el error de la superficie es de algo más de 15 m2.
En una medida de precisión normal, el error es lo suficientemente pequeño como para poder sustituir la curva por la recta tangente a la curva. La relación entre el error de y y el error de x será entonces la pendiente de la curva en el punto de interés. Como el valor del lado es 8, el error de la superficie (y) es 16 veces el error del lado.
En un caso más general tendremos dos o más variables en lugar de sólo una. Por ejemplo, si la parcela anterior es rectangular en vez de cuadrada, la superficie es función de dos variables: la base (x) y la altura (y). La medida de cada una de estas dos variables tendrá un cierto error, que se propagará al valor de la superficie: S=x.y.
La teoría de errores constituye una rama del conocimiento científico que, a los efectos de la enseñanza, queda en un terreno intermedio entre el de las teorías científicas y el de la práctica experimental.
En cursos teóricos (Teoría de los Números Aproximados, Cálculo Diferencial, Estadística) se analizan, en forma disgregada, elementos de la Teoría de Errores (confiabilidad de las cifras, cálculo con cantidades pequeñas, desviaciones probables, etc.), con un enfoque más cercano a los muestreos poblacionales de parámetros sociales y económicos que al de la instrumentación científica. Por otra parte, en los laboratorios docentes la preocupación fundamental de los profesores radica en las técnicas Instrumentales y en la verificación experimental de leyes, analizadas en los cursos teóricos de la ciencia correspondiente. En cada experimento se sugiere al estudiante valorar los errores que más influyen en él, explicitando estos en cada caso: a veces, errores casuales, a veces, sistemáticos rectificables; otras veces, errores de apreciación de los instrumentos; otras, los de método. Y el estudiante va adquiriendo una visión fragmentada de todos los tipos de errores, pero sin una clara noción de cómo se vinculan, y cuándo tener en cuenta sólo a unos y no a los otros.
Los métodos para procesar todos estos tipos de errores se van analizando también disgregadamente, de acuerdo con cada experimento específico estudiado, y de acuerdo con el enfoque del profesor de cada laboratorio.
En fin de cuentas, el modo de evaluar los errores y el de procesarlos es, a veces, tan variado como lo sean los profesores por los que ha pasado un estudiante. Y se espera que éste, ya sea científico o ingeniero, adquiera la formación correcta en el tratamiento de los errores de medición.
Un paso fundamental en la enseñanza de un tema, o asignatura, con enfoque sistemático, es dejar establecida al inicio, en forma de recuadro, la estructura completa del contenido a tratar, que muestre los vínculos y engranajes de unas partes con otras, y explicar, sin profundidades, en qué consiste cada parte. Después, durante el curso, se estudia cada parte consignada en el recuadro inicial, que se retoma durante el curso tantas veces como se requiera.

Incertidumbre de las Medidas
La limitación de los elementos físicos disponibles para realizar un sistema de medida hacen que las señales de salida discrepen de las que se obtendrían con un sistema ideal. Estas discrepancias se denominan errores y, dado que algunas de ellas son inevitables, el objetivo es reducirlas de modo que a partir de la salida se pueda determinar el valor de la entrada con una incertidumbre aceptable. El número de cifras con que se exprese un resultado debe concordar con la incertidumbre que tenga asociada.
Los errores de un sistema se determinan a partir de su calibración, que consiste en aplicarle entradas conocidas y comparar su salida con la obtenida con un sistema de medida de referencia, más exacto.
Las medidas nunca permiten obtener el “verdadero valor” de la magnitud que se mide. Esto es debido a multitud de razones. Las más evidentes son las imperfecciones, inevitables en un cierto grado, de los aparatos y de nuestros sentidos. El “verdadero valor” de una magnitud no es accesible en la realidad y por ello resulta más propio hablar de estimaciones, medidas o aproximaciones del valor de una magnitud. Independientemente de estas consideraciones, en el ámbito de la Instrumentación se sabe que no tiene sentido hablar del valor de una magnitud, sino sólo de la probabilidad de obtener uno u otro valor en una determinada medida de esta magnitud. Esto no es el resultado de las imperfecciones de los aparatos, sino de la propia esencia de la naturaleza. Este carácter probabilístico de las magnitudes se hace patente a nivel microscópico.
La consecuencia de las consideraciones anteriores, es que toda medida es incierta o está dotada de un cierto grado de incertidumbre. Es esencial estimar ésta incertidumbre, primero porque el conocimiento de la incertidumbre aumenta la información que proporciona la medida, y segundo, porque este conocimiento permite manejar las medidas con la prudencia que dicta el conocimiento de la confianza que nos merecen.
Cuando se exprese el resultado de una medida es pues necesario especificar tres elementos: número, unidad e incertidumbre. La ausencia de alguna de ellas elimina o limita la información que proporciona.
Según su naturaleza los errores pueden ser sistemáticos o aleatorios.
Error Sistemático
Un error sistemático tiene siempre la misma amplitud cuando las condiciones del sistema son las mismas, o bien varía de acuerdo con una ley conocida cuando una de dichas condiciones cambia de una forma predeterminada.
Pueden surgir de emplear un método inadecuado, un instrumento defectuoso o bien por usarlo en condiciones para las que no estaba previsto su uso. Por ejemplo, emplear una regla metálica a una temperatura muy alta, puede introducir un error sistemático si la dilatación del material hace que su longitud sea mayor que la nominal. En este caso, todas las medidas pecarán (sistemáticamente) por defecto. El error podría evitarse eligiendo un material de coeficiente de dilatación bajo o controlando la temperatura a la que se mide.
Un error sistemático por ejemplo, son las resistencias reales del modelo del sistema de medida y que se suman o interfieren en el proceso de medida.
Medir temperaturas con un termómetro graduado en grados Farenhait, suponiendo por equivocación que está graduado en grados Celsius, introduce también un error sistemático en la medida. El error se evita en este caso recabando información sobre la escala del termómetro.
Los errores sistemáticos no son objeto de la teoría de errores. Realmente son equivocaciones que pueden y deben evitarse, empleando métodos e instrumentos de medida correctos y adecuados a los fines que se deseen obtener.
Error Aleatorio
Un error aleatorio tiene una magnitud que cambia de unas a otras ocasiones a pesar de que las condiciones del sistema sean las mismas.
Los errores aleatorios se manifiestan cuando se mide repetidamente la misma magnitud con el mismo instrumento y el mismo método, y presentan las siguientes propiedades:
Los errores aleatorios positivos y negativos de igual valor absoluto tienen la misma probabilidad del producirse.
Los errores son tanto menos probables cuando mayor sea su valor.
Al aumentar el número de medidas, la media aritmética de los errores aleatorios de una muestra tiende a cero.
Para un método de medida determinado, los errores aleatorios no exceden de cierto valor. Las medidas que lo superan deben repetirse y, en su caso, estudiarse por separado.
La calibración permite corregir los errores sistemáticos y estimar la magnitud de los errores aleatorios (pero no corregirlos).
Errores Estáticos y Errores Dinámicos
Según que se manifiesten cuando las señales de entrada son lentas o rápidas, los errores se denominan estáticos o dinámicos.
Un error estático afecta a las señales lentas, por ejemplo de frecuencia inferior a 0,01 Hz. Un error dinámico afecta a las señales rápidas, y es una consecuencia de la presencia de elementos que almacenan energía. Dado que en la respuesta dinámica se consideran dos fases, la respuesta transitoria y la respuesta estacionaria, se habla de error dinámico transitorio y error dinámico estacionario.
El error dinámico de un sistema depende de su orden y de la forma de la señal de entrada. Las señales consideradas habitualmente son el escalón, la rampa y las senoidales. Los sistemas de orden cero no tienen error dinámico. Los sistemas de primer y de segundo orden tienen un error dinámico para las entradas en rampa y senoidales, incluso en régimen estacionario, y tienen un error dinámico para las entradas en escalón sólo durante la fase transitoria. En los sistemas de segundo orden la fase transitoria dura tanto más cuanto menor sea el amortiguamiento. El error dinámico para entradas senoidales incluye un retardo y un error de amplitud, pero normalmente al hablar de error dinámico se suele sobrentender el error de amplitud.
Forma de expresar los errores
La magnitud de un error se puede expresar como error absoluto, como error relativo o como error referido a fondo escala. El error absoluto es la diferencia entre el resultado y el verdadero valor (o valor ideal). El error relativo es el cociente entre el error absoluto y el verdadero valor. El error absoluto se expresa a veces como porcentaje de una magnitud de referencia, por ejemplo el valor de fondo de escala. La elección de una u otra forma de expresión depende del tipo de error.
Error Absoluto
Por motivos obvios, y por su propia naturaleza, no es posible determinar exactamente un error. En el mejor de los casos, puede llegarse a una estimación de ese error. Cuando el resultado de una medida se expresa por:
lo que se quiere decir es que la magnitud medida se encuentran en el intervalo con una determinada probabilidad. Con una medida logramos acotar el intervalo de valores en los que se encuentra la magnitud que pretendemos medir, pero siempre con una determinada probabilidad. Es evidente que el error expresado por es una magnitud de la misma clase que la medida y se expresa por tanto con la misma unidad. También es claro que en las medidas de calidad normal el error debe ser mucho menor que el valor nominal, x. Por definición es siempre positivo.
Error Relativo
El error definido arriba se llama error absoluto. Tiene también interés el error relativo, que se define como el cociente del error absoluto, dividido por x.

En medidas de una cierta calidad el error relativo debe ser mucho menor que la unidad. Frecuentemente se expresa multiplicado por 100, con lo que aparece en tanto por ciento del valor medido:

Cifras significativas
Se considera que las cifras significativas de un número son aquellas que tienen significado real o aportan alguna información. Las cifras no significativas aparecen como resultado de los cálculos y no tienen significado alguno. Las cifras significativas de un número vienen determinadas por su error. Son cifras significativas aquellas que ocupan una posición igual o superior al orden o posición del error.
Por ejemplo, consideremos una medida de longitud que arroja un valor de 5432,4764 m con un error de 0,8 m. El error es por tanto del orden de décimas de metro. Es evidente que todas las cifras del número que ocupan una posición menor que las décimas no aportan ninguna información. En efecto, ¿qué sentido tiene dar el número con precisión de diezmilésimas si afirmamos que el error es de casi 1 metro?. Las cifras significativas en el número serán por tanto las que ocupan la posición de las décimas, unidades, decenas, etc, pero no las centésimas, milésimas y diezmilésimas. Cuando se expresa un número debe evitarse siempre la utilización de cifras no significativas, puesto que puede suponer una fuente de confusión. Los números deben redondearse de forma que contengan sólo cifras significativas. Se llama redondeo al proceso de eliminación de cifras no significativas de un número.
Una última forma de expresar el error de un número consiste en afirmar que todas sus cifras son significativas. Esto significa que el error es del orden de media unidad de la última cifra que se muestra. Por ejemplo, si el resultado de una medida de longitud es de 5432,8 m, y afirmamos que todas las cifras son significativas, quiere decirse que el error es del orden de 0,5 m, puesto que la última cifra mostrada es del orden de las décimas de metro.
¿Cómo pueden determinarse las cifras significativas a partir del número que expresa el error?. Hay que tener siempre presente que todo error es una estimación y está por tanto sujeto a su vez a una incertidumbre, generalmente grande. Por esto no tiene sentido especificarlo con excesiva precisión. Salvo casos excepcionales, se expresará con una sola cifra significativa. Sobre cómo redondear números, consultar la sección.
Redondeo de Números
Hemos visto que todos los números resultantes de una medida tienen una cierta incertidumbre. Es necesario eliminar de estos números aquellas cifras que carecen de significado porque el error es mayor que lo que estas cifras significan.
Las reglas que se emplean en el redondeo de números son las siguientes:
Ø Si la cifra que se omite es menor que 5, se elimina sin más.
Ø Si la cifra eliminada es mayor que 5, se aumenta en una unidad la última cifra retenida.
Ø Si la cifra eliminada es 5, se toma como última cifra el número par más próximo; es decir, si la cifra retenida es par se deja, y si es impar se toma la cifra superior.
Ø Algunos ejemplos. Si redondeamos 3,678 a tres cifras significativas, el resultado es 3,68, que está más cerca del original que 3,67. En cambio si el número a redondear, también a tres cifras, fuera 3,673, quedaría 3,67 que es más próximo al original que 3,68. Para redondear 3,675, según la tercera regla, debemos dejar 3,68.
Las dos primeras reglas son de sentido común. La tercera es un convenio razonable porque, si se sigue siempre, la mitad de las veces redondeamos por defecto y la mitad por exceso.
Cuando los números a redondear sean grandes, las cifras eliminadas se sustituyen por ceros. Por ejemplo, el número 3875 redondeado a una cifra significativa resulta 4000. En este caso suele preferirse la notación exponencial, puesto que si escribimos ``4000'' puede no estar claro si los ceros son cifras significativas o no.
Errores de cero, ganancia y de no linealidad
Según su efecto en la característica de transferencia, los errores pueden ser de cero, de ganancia y de no linealidad.
Un error de cero permanece constante con independencia del valor de la entrada. Un error de ganancia es proporcional al valor de la entrada. Un error de no linealidad hace que la característica de transferencia se aparte de una línea recta (suponiendo que sea ésta la característica ideal).
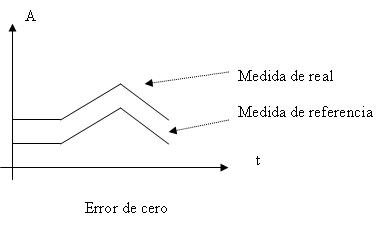
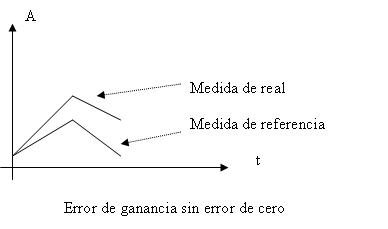
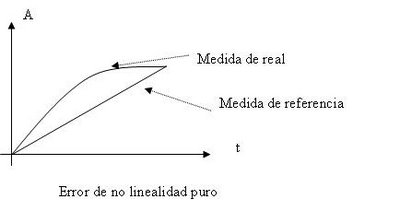
Los errores de cero y de no linealidad se suelen expresar como errores absolutos. Los errores de ganancia se suelen expresar como errores relativos. Dado que normalmente hay errores de todos los tipos, la expresión de la incertidumbre o error total suele incluir un término constante y otro que depende del resultado.
Estimación del Error de una Medida Directa
La estimación del error de una medida tiene siempre una componente subjetiva. En efecto, nadie mejor que un observador experimentado para saber con buena aproximación cuál es el grado de confianza que le merece la medida que acaba de tomar. No existe un conjunto de reglas bien fundadas e inalterables que permitan determinar el error de una medida en todos los casos imaginables. Muchas veces es tan importante consignar cómo se ha obtenido un error como su propio valor.
Sin embargo, la aplicación de algunos métodos estadísticos permite objetivar en gran medida la estimación de errores aleatorios. La estadística permite obtener los parámetros de una población (en este caso el conjunto de todas las medidas que es posible tomar de una magnitud), a partir de una muestra (el número limitado de medidas que podemos tomar).
Mejor valor de un conjunto de Medidas
Supongamos que medimos una magnitud un número n de veces. Debido a la existencia de errores aleatorios, las n medidas serán en general diferentes.
El método más razonable para determinar el mejor valor de estas medidas es tomar el valor medio. En efecto, si los errores son debidos al azar, tan probable es que ocurran por defecto como por exceso, y al hacer la media se compensarán, por lo menos parcialmente. El valor medio se define por:
Ø Si la cifra que se omite es menor que 5, se elimina sin más.
Ø Si la cifra eliminada es mayor que 5, se aumenta en una unidad la última cifra retenida.
Ø Si la cifra eliminada es 5, se toma como última cifra el número par más próximo; es decir, si la cifra retenida es par se deja, y si es impar se toma la cifra superior.
Ø Algunos ejemplos. Si redondeamos 3,678 a tres cifras significativas, el resultado es 3,68, que está más cerca del original que 3,67. En cambio si el número a redondear, también a tres cifras, fuera 3,673, quedaría 3,67 que es más próximo al original que 3,68. Para redondear 3,675, según la tercera regla, debemos dejar 3,68.
Las dos primeras reglas son de sentido común. La tercera es un convenio razonable porque, si se sigue siempre, la mitad de las veces redondeamos por defecto y la mitad por exceso.
Cuando los números a redondear sean grandes, las cifras eliminadas se sustituyen por ceros. Por ejemplo, el número 3875 redondeado a una cifra significativa resulta 4000. En este caso suele preferirse la notación exponencial, puesto que si escribimos ``4000'' puede no estar claro si los ceros son cifras significativas o no.
Errores de cero, ganancia y de no linealidad
Según su efecto en la característica de transferencia, los errores pueden ser de cero, de ganancia y de no linealidad.
Un error de cero permanece constante con independencia del valor de la entrada. Un error de ganancia es proporcional al valor de la entrada. Un error de no linealidad hace que la característica de transferencia se aparte de una línea recta (suponiendo que sea ésta la característica ideal).



Los errores de cero y de no linealidad se suelen expresar como errores absolutos. Los errores de ganancia se suelen expresar como errores relativos. Dado que normalmente hay errores de todos los tipos, la expresión de la incertidumbre o error total suele incluir un término constante y otro que depende del resultado.
Estimación del Error de una Medida Directa
La estimación del error de una medida tiene siempre una componente subjetiva. En efecto, nadie mejor que un observador experimentado para saber con buena aproximación cuál es el grado de confianza que le merece la medida que acaba de tomar. No existe un conjunto de reglas bien fundadas e inalterables que permitan determinar el error de una medida en todos los casos imaginables. Muchas veces es tan importante consignar cómo se ha obtenido un error como su propio valor.
Sin embargo, la aplicación de algunos métodos estadísticos permite objetivar en gran medida la estimación de errores aleatorios. La estadística permite obtener los parámetros de una población (en este caso el conjunto de todas las medidas que es posible tomar de una magnitud), a partir de una muestra (el número limitado de medidas que podemos tomar).
Mejor valor de un conjunto de Medidas
Supongamos que medimos una magnitud un número n de veces. Debido a la existencia de errores aleatorios, las n medidas serán en general diferentes.
El método más razonable para determinar el mejor valor de estas medidas es tomar el valor medio. En efecto, si los errores son debidos al azar, tan probable es que ocurran por defecto como por exceso, y al hacer la media se compensarán, por lo menos parcialmente. El valor medio se define por:
y este es el valor que deberá darse como resultado de las medidas.
Dispersión y Error. Desviación Estándar
Evidentemente, el error de la medida debe estar relacionado con la dispersión de los valores; es decir, si todos los valores obtenidos en la medición son muy parecidos, es lógico pensar que el error es pequeño, mientras que si son muy diferentes, el error debe ser mayor.
Adoptando un criterio pesimista, podría decirse que el error es la semi diferencia entre el valor máximo y el mínimo.
Dispersión y Error. Desviación Estándar
Evidentemente, el error de la medida debe estar relacionado con la dispersión de los valores; es decir, si todos los valores obtenidos en la medición son muy parecidos, es lógico pensar que el error es pequeño, mientras que si son muy diferentes, el error debe ser mayor.
Adoptando un criterio pesimista, podría decirse que el error es la semi diferencia entre el valor máximo y el mínimo.
Este error es sin embargo excesivamente grande, además de que el criterio utilizado es discutible. Parece más apropiado tomar como error la desviación media, es decir, el valor medio de la diferencia de los datos respecto al valor central. Sin embargo, como los datos difieren tanto por defecto como por exceso del valor medio, tal desviación se aproximaría a cero. Para evitarlo suele tomarse, no el valor medio de las desviaciones, sino el valor medio de las desviaciones al cuadrado. De esta forma todos los sumandos son positivos. Para que la unidad de este número sea homogénea con la de los datos, se extrae la raíz cuadrada. El valor resultante se llama desviación típica o desviación estándar del conjunto de datos.

Cuando el número de datos es pequeño, suele preferirse el cálculo de la desviación estándar por la ecuación:

La primera suele llamarse desviación estándar de población, y la segunda desviación estándar muestral. Uno de los motivos de preferir la segunda, es que cuando medimos una sola vez, el resultado de la ecuación 6 es , es decir un número indefinido. Efectivamente, midiendo una magnitud una sola vez, no tenemos información alguna sobre su error, y por lo tanto éste debe permanecer indefinido. Sin embargo la expresión 5 conduciría a un error nulo.
Las dos expresiones se emplean, aunque en la práctica, y si el número de medidas es grande, la diferencia entre emplear una u otra es muy pequeña. La más empleada es la segunda, ecuación 6 y es la que usaremos nosotros.
Significado de la Desviación Estándar. La Distribución Normal
Los valores de la desviación estándar que hemos calculado en la sección anterior, son realmente estimadores de este parámetro. El conjunto de las medidas de una magnitud, siempre que exista un error accidental, pueden caracterizarse por medio de una distribución estadística. Cuando el error es debido a un gran número de pequeñas causas independientes, la distribución se aproxima a la llamada distribución normal.
La forma de representar en estadística una distribución es representando en abscisas el conjunto de valores que pueden obtenerse en una medida y en ordenadas la probabilidad de obtenerlos. En el caso de que la magnitud medida varíe de forma continua, en ordenadas se representa la probabilidad por unidad de intervalo de la magnitud medida.
La función de densidad de la distribución normal tiene el aspecto reflejado en la figura 4. Recibe también el nombre de campana de Gauss debido a su forma. Está caracterizada por dos parámetros: media y desviación estándar. La media es el valor que con mayor probabilidad aparecerá en una medida. La desviación estándar refleja lo abierta o cerrada que es la campana de Gauss correspondiente. Una distribución muy cerrada se corresponde con una serie de medidas muy poco dispersas, y por tanto con poco error. Por el contrario si la distribución es abierta, la desviación estándar es grande.
Una de las propiedades de la distribución normal es que la probabilidad que encierra en el intervalo es del 68.3 % aproximadamente. Es decir, es de esperar que el 68.3 % de las medidas de una magnitud estén comprendidas en ese intervalo. Dicho de otra forma, si medimos una magnitud un número grande de veces, el 68.3 % de los valores obtenidos estarán comprendidos en el entorno de una desviación estándar en torno a la media. La probabilidad se amplía al 95.4 % y al 99.7 % si consideramos los intervalos y respectivamente.

Figura 4: Función de densidad de una distribución normal
El error expresado por la desviación estándar tiene por tanto un significado probabilístico: hay una probabilidad del 68% de que una medida esté en el entorno de una desviación estándar alrededor de la media.
La distribución normal aparece con frecuencia en las medidas de magnitudes, pero no siempre. La distribución de una serie de medidas se aproxima a una normal siempre y cuando la fuente de error sea la superposición de muchas pequeñas causas independientes. Si hay una o varias causas de error predominantes o si las causas de error no son independientes, se dice que las medidas presentan un sesgo, y la distribución puede muy bien ser otra. Es muy frecuente encontrar distribuciones de medidas no simétricas, con dos o más máximos, etc.
Conviene insistir finalmente en que no es posible determinar la media y la desviación estándar de una distribución, sino solamente estimarlas.
Medidas sin dispersión. Error de lectura o instrumental
En ocasiones la repetición de la medida de una magnitud conduce siempre al mismo valor. Como ejemplo, consideremos la medida de la longitud de un objeto con una regla graduada en milímetros. Si la medida se realiza con cierta atención, todas las medidas del objeto proporcionan el mismo valor. Es evidente que en este caso la teoría anterior no resulta aplicable, porque al ser nula la dispersión, la desviación estándar resulta igual a cero. En estos casos, la fuente de error no está en la superposición de muchas causas aleatorias, sino en la sensibilidad del aparato de medida.
En efecto, el hecho de que todas las medidas sean iguales no indica en general que no haya error accidental, sino que éste es demasiado pequeño para quedar reflejado en el aparato. En el ejemplo anterior, si el error accidental de las medidas es del orden de 0,001 mm es evidente que la regla no podrá apreciarlo, resultando todas las medidas iguales. En estos casos es necesario estimar el error debido a la sensibilidad finita del aparato de medida.
Se llama sensibilidad de un aparato a la mínima variación de la magnitud medida que es capaz de detectar. En los instrumentos analógicos coincide frecuentemente con la mínima división de la escala. En el ejemplo anterior la sensibilidad de la regla es de 1 mm.
Suele llamarse apreciación al máximo error que puede cometerse debido a la sensibilidad del aparato. Generalmente se considera como la mitad de la sensibilidad. Esto puede comprenderse con un ejemplo. Supongamos un voltímetro de 0,1 V de sensibilidad, cuya aguja indica una tensión comprendida entre 2,1 V y 2,2 V, es decir, la aguja señala un punto intermedio entre las dos marcas o divisiones de la escala. Si el aparato está bien diseñado, una persona con apreciación visual media debe ser capaz de decidir si la aguja está más cerca de 2,1 V o de 2,2 V. Cometeremos el máximo error cuando la aguja se encuentre justamente en el centro de las dos divisiones. En tal caso el error de dar como lectura 2,1 V o 2,2 V es de 0,05 V, es decir la mitad de la sensibilidad.
Hemos visto que cuando el error instrumental es mucho mayor que el accidental, éste queda enmascarado por aquel. El efecto inverso es también posible. Por tanto, en los casos en que el error accidental de una medida sea mucho mayor que el instrumental, sólo consideraremos el error accidental.
Propagación de Errores
Las operaciones matemáticas con números inciertos dan lugar a resultados también inciertos, y es importante poder estimar el error de los resultados a partir de los errores de los números con los que se opera.
Consideremos un ejemplo sencillo para ilustrar este tema. Supongamos que se mide el lado (x) de una parcela de terreno cuadrada, y a partir de esta medida quiere obtenerse su superficie (y). La medida del lado llevará aparejada un error, que puede ser de origen accidental, instrumental o combinación de ambos. Admitamos que el lado mide 8 m y que el error es de 1 m. El valor de la superficie es por tanto de 64 m2, y estamos interesados en estimar su error.
El error en la medida del lado puede interpretarse como el radio de un entorno alrededor del valor nominal, en cuyo interior estará el valor del lado con una determinada probabilidad. Si proyectamos este entorno sobre la curva obtendremos otro entorno en el eje de ordenadas que representa el error de la superficie. Inspeccionando la figura llegamos a la conclusión de que el error de la superficie es de algo más de 15 m2.
En una medida de precisión normal, el error es lo suficientemente pequeño como para poder sustituir la curva por la recta tangente a la curva. La relación entre el error de y y el error de x será entonces la pendiente de la curva en el punto de interés. Como el valor del lado es 8, el error de la superficie (y) es 16 veces el error del lado.
En un caso más general tendremos dos o más variables en lugar de sólo una. Por ejemplo, si la parcela anterior es rectangular en vez de cuadrada, la superficie es función de dos variables: la base (x) y la altura (y). La medida de cada una de estas dos variables tendrá un cierto error, que se propagará al valor de la superficie: S=x.y.



0 Comments:
Post a Comment
<< Home